
This paper provides a comprehensive overview of the applications of game theory in deep learning. Today, deep learning is a fast-evolving area for research in the domain of artificial intelligence. Alternatively, game theory has been showing its multi-dimensional applications in the last few decades. The application of game theory to deep learning includes another dimension in research. Game theory helps to model or solve various deep learning-based problems. Existing research contributions demonstrate that game theory is a potential approach to improve results in deep learning models. The design of deep learning models often involves a game-theoretic approach. Most of the classification problems which popularly employ a deep learning approach can be seen as a Stackelberg game. Generative Adversarial Network (GAN) is a deep learning architecture that has gained popularity in solving complex computer vision problems. GANs have their roots in game theory. The training of the generators and discriminators in GANs is essentially a two-player zero-sum game that allows the model to learn complex functions. This paper will give researchers an extensive account of significant contributions which have taken place in deep learning using game-theoretic concepts thus, giving a clear insight, challenges, and future directions. The current study also details various real-time applications of existing literature, valuable datasets in the field, and the popularity of this research area in recent years of publications and citations.

Avoid common mistakes on your manuscript.
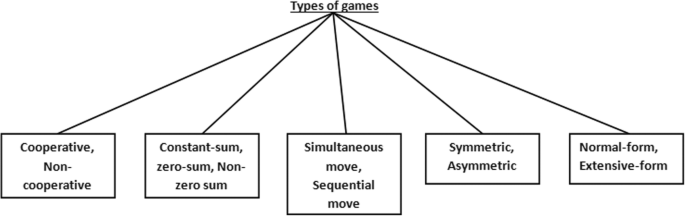
Game theory is an essential field for research, and it helps to choose the suitable strategy of the players in a game. It has several applications in various domains. Game theory has significant applications in technology, especially concerning computer science, electronics, aerospace engineering, etc. [90, 91, 96, 99, 100]. Different types of games are briefed in Fig. 1. Alternatively, Deep Learning is the study of various learning algorithms that uses multiple layers of non-linear processing units. The output of the previous layer is taken as input by each successive layer. Deep learning algorithms are primarily classified into three categories, e.g., supervised, semi-supervised and unsupervised. Deep Learning algorithms implement higher-level features that are extracted from lower-level features. The depth in neural networks plays an essential part in the outcome of the model. The framework of the neural networks can represent dynamic environments, and similarly, dynamic environments can further be presented as games [37, 72].
Artificial intelligence has adapted the game theory to solve or model various real-time problems, and it is observed that the performance is improved while applying game theory [43, 76, 124, 148]. This paper establishes the connection of deep learning algorithms with game theory. The applications of evolutionary computing and swarm intelligence are discussed in [20]. This paper mainly focuses on applications of game theory to solve GAN models. GAN has received a tremendous response from several research communities because of its complex problem-solving abilities and performance improvement [19, 36, 130].
The multilayer neural network comprises any number of unit neurons and may determine multimodal output functions. The multimodality nature of the output function creates hardships to optimize deep neural network models. Strategic Deep Learning is a defying game task [62, 84, 136, 141, 151]. Table 1 shows research articles in game theory, deep learning, and their collaborative research as per the records obtained from various databases. In a nutshell, the contribution of the paper is as follows:
Players are the critical components of a game. They participate in a game intending to achieve certain goals. The nature of interaction among the players can be primarily classified into two types: cooperative and non-cooperative. Two or more than two players can take part in a game. The players always aim to maximize the overall payoff of the whole group.
In a game, strategies are a sequence of actions chosen by the players. The strategies can also be fundamentally classified into two types, cooperative and non-cooperative, based on players’ goals. The paramount of a game is to determine suitable strategies for players.
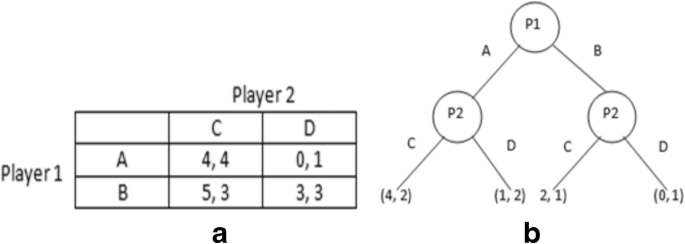
The payoffs of players represent the rewards or penalties for choosing their respective strategies. In cooperative games, players aim to improve the overall payoffs of a group. In contrast, the players aim to maximize their self-payoff (without considering the overall payoff of the group) in non-cooperative games. The game planners formulate the payoff functions. Let StI represents all possible strategies for player I. If there are m number of players, then, possible combinations of strategies for player I is St1 × St2…Stm. So, the payoff function can be represented as util(St1 × St2…Stm).
Best response strategies denote the most favorable outcomes for a player considering all the strategies for opponents. The players in a game usually prefer to choose the best response strategies. NE is determined based on the best response strategies for players. Let best response strategy for player I be represented asbrI(.). Thus, considering a set of opponent’s strategiesx−I, brI(x−I) denotes player I’s best response to x−I.
It is a stable state where players cannot earn more profits by unilaterally deviating from their strategies. Players can have a pure or mixed strategy equilibrium in a game.
Let a game with m players be denoted by (St, util), StI represents strategies for player I, St = St1 × … × Stm represents strategy combinations andutil(x) = (util1(x), …, utilm(x)) represents the utility or payoff function, wherexϵSt. xIandx−I are the strategy combination for player I and others except for player I, respectively. When each player Iϵ1, …, mcomputes the strategy xI from the strategy-profilex = x1, …, xm, then, the player I gets a payoffutilI(x). A strategy profile x ∗ ϵSt is a NE if the following condition is satisfied
$$\forall I,Mixed equilibrium is computed for those scenarios, where the players mix their strategies with uncertainties, and the mixed equilibrium is computed based on the expected payoffs of respective players [92].
In cooperative games, the reward of each player is computed by a function called Shapleyfunction. The Shapley value \(<\Phi>_(v)\) for each player Si, 1 ≤ i ≤ N is computed based on its individual contribution to a coalition, where N represents the player count. The Shapley value [116] for each player is calculated by the equation given below.
In the above equation, S represents a set of N players (|S| = N), C denotes a group (|C| = c) and C is a subset of S\Si>, \(\frac<\mathrm!\left(\mathrm-\mathrm-1\right)><\mathrm!>\) denotes the uncertainty in a permutation, the contributors of C are ahead of the individual player Si and (v(C ∪ Si>) − v(C)) denotes the individual contribution of a player Si in the group C, where the rewards of all groups are initially determined. In this way, the Shapley function \(<\Phi>_(v)\) yields the Shapley value of a player Si for a particular group. A player having the highest Shapley value is the most significant contributor in a group.
In 1928, John Von Neumann introduced the Minimax theorem, which opens the door for conventional game theory. For a two-player, zero-sum, simultaneous move finite game, there must be a value and exists an equilibrium point for both the players [126]. The equilibrium point can be determined by applying pure or mixed strategies by either one or both the players. Let’s assume that x and y are strategies of two players and v is the value of the game. Then, the minimax theorem can be formulated as
$$ x\in X,y\in Y\max \kern.5em \min f\left(x,y\right)=y\in Y,x\in X\ \min \kern.5em \max f\left(x,y\right)=v $$
Deep learning is an advanced part of machine learning algorithms based on artificial neural networks and various learning methods, i.e., supervised, unsupervised, and reinforcement. There are well-known deep learning architecture and techniques. Deep learning models use multiple layers in an artificial neural network to extract significant characteristics from the unprocessed data. Graphics Processing Units (GPUs) are required to perform high-power computation on complex deep learning architectures. Deep learning has immense applications in multi-dimensional fields such as speech recognition, computer vision, audio recognition, natural language processing, medical image analysis, games, etc.
In recent times, deep learning has received tremendous responses from various fields. Robust deep learning architectures bring significant improvement in the performance of multiple models. They can solve or model various complex problems because of their robustness. In most cases, it is observed that deep learning architectures outperform other existing models. The most popular deep learning architectures are the convolutional neural network, recurrent neural network, generative adversarial network, deep belief network, autoencoder, residual neural network, etc. This paper primarily studies generative adversarial neural networks because of their architecture, where game-theoretic techniques can be easily applied. In the future, we may explore possibilities of applications of game theory in other deep learning architectures.
The convolutional neural network, a significant type of deep learning architecture, is best known for its vast capabilities when analyzing visual imagery. They comprise regularized versions of complicated multilayer perceptrons (usually fully connected networks). A CNN has three layers, input, hidden, and output. The hidden layers are mainly convolutional layers that convolve with multiplication or other product, and the activation function is commonly a RELU layer. CNNs were inspired by the works [32, 59, 60].
Recurrent Neural Network is a category of advanced artificial neural networks. A directed graph with a temporal sequence is what we get when there is a connection between the nodes. Temporal dynamic behavior is exhibited in RNN. Using internal states, RNNs have capabilities to process inconsistent range sequences of inputs. They are powerful enough because having a distributed hidden state makes them capable of storing huge amounts of information regarding the past and non-linear dynamics, acknowledging them to revise their hidden state in complex ways [39, 111, 146].
Long Short-Term Memory, applied in deep learning, belongs to the family of recurrent neural networks. Its specialty lies in the fact that along with feed-forward neural networks, it has feedback connections too. A general LSTM architecture constitutes a cell, an input gate, an output gate, and a front gate. The utility of a cell is to store values over irregular periods, and all gates examine the flow of data entering into and exiting out of the cell. LSTM networks are best applicable in categorizing, processing, and predicting based on time series data [15, 54].
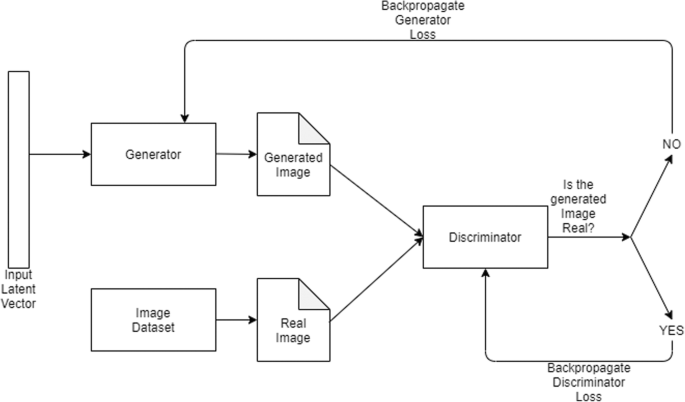
Generative adversarial network (GAN), a type of deep learning architecture, was invented in 2014 by Ian Goodfellow [36]. Here, two neural networks challenge amongst themselves in a game (initially given a training set). The theory of GAN is to train images that can generate new images that look accurate to human eyes. GANs were originally modeled for unsupervised learning, but they are broadly used in reinforcement learning, semi-supervised learning, and fully supervised learning.
GAN layered architecture is represented in Fig. 3. Let’s introduce the variables and parameters related to the GAN model
Parameters of the discriminator
Parameters of generator
Input noise distribution
Original data distribution
The final loss function for the discriminator can be written as
$$Alternatively, the generator is competing with the discriminator. The final loss function for the generator can be written as
$$Both the equations can be combined and rewritten as
$$\undersetThe above equation represents a single data point. For an entire dataset, we can write the equation as follows:
A deep belief network, a type of deep learning architecture, is a probabilistic generative graphical model. They are constructed from several layers of stochastic, latent variables with binary values called hidden layers or feature identifiers. The two compelling features of deep neural networks are:
Autoencoder, a distinctive category of artificial neural network utilized in learning efficient data coding through unsupervised techniques. Autoencoders target to learn an encoding for a set of given data and to reduce dimensions in data by training the given network to ignore “noise.” They can probably encode a provided input to represent smaller dimensions, being a data-compression model. Later, decoders can then reconstruct the input back from the encoded version [125, 147].
Residual neural networks, abbreviated as ResNet, are artificial neural networks of a particular type inspired by the pyramidal cells of the animal cerebral cortex. Residual neural networks perform this by applying skip connections or shortcuts to jump through a few layers. ResNet models are achieved using double/triple layer skips consisting of nonlinearities (ReLU) and batch normalization in between [46]. An extra new weight matrix may be used to learn the skip weights. Such architectures are known as HighwayNets [121]. Architecture with several parallel skips is termed as DenseNets [57].
“The RBF network model is motivated by the locally tuned response observed in biologic neurons. Neurons with a locally tuned response characteristic can be found in several parts of the nervous system, such as cells in the auditory system that are selective to small bands of frequencies [114]”.
“MLPs belong to the class of feedforward neural networks with multiple layers of perceptrons that have activation functions. MLPs consist of an input layer and an output layer that is fully connected. They have the same number of input and output layers but may have multiple hidden layers and can be used to build speech recognition, image recognition, and machine-translation software [8].”
“The SOM algorithm distinguishes two stages: the competitive stage and the cooperative stage. In the first stage, the best matching neuron is selected. In the second stage, neuron weights are not modified independently but as topologically-related subsets on which similar kinds of weight updates are performed [66].”
Dropout is adapted as a technique to overcome overfitting problems in a neural network. It addresses both issues – training and testing computations. Effectively, it allows the training of several neural networks without any significant computational overhead. Also, it gives an efficient approximate way of combining exponentially many different neural networks. In the training phase, dropping out refers to dropping out units(neurons) of a certain set of randomly chosen neurons. The dropped out units are not further considered during a forward and backward pass. Temporarily removes a node and all its incoming/outgoing connections, resulting in a thinned network [49, 50].
ReLU is an activation function broadly used in various deep learning architectures. It is a non-linear activation function used for both types of networks, i.e., multiple-layer neural networks and deep neural networks. The function for any negative input returns zero. Alternatively, x is returned by the function for any positive input x. So, the simplified form of the function is f(x) = max(0, x).
In recent times, a sigmoid and hyperbolic tangent is replaced by the ReLU function. The main reason for the popularity of the ReLU function is its ability to make the training speed of deep neural networks faster than other conventional activation functions. A significant feature of ReLU is the derivative of this function is 1 for positive input. Deep neural networks can save additional time for calculating error terms due to a constant during the training phase. The extensive use of ReLU is shown in [34].
Stochastic gradient descent is one of the powerful algorithms used in several machine learning and deep learning models. It is the basis of neural networks. It is an essential iterative algorithm. The functionalities of the gradient descent algorithm are as follows: it starts from an arbitrary point on a function. It moves down its slope in several steps/iterations until it reaches the minimum point of the given function. The algorithm is modified by including a random probability, called Stochastic Gradient Descent. In this algorithm, a set of samples is randomly chosen from the whole data set in each iteration. If we consider a large dataset, the programmer may require using many samples in each iteration while using the Gradient Descent algorithm. The task needs to be performed for each iteration until the minima are found, which is the main challenge in the Gradient Descent algorithm. Computational complexity is a significant concern in this algorithm. Stochastic Gradient Descent is introduced as a solution to this problem. SGD reduces the sample size. It takes only a single sample to perform the task for each iteration. Therefore, the sample is randomly mixed and chosen for completing the task for the iteration. The backbone of the SGD is to consider the gradient of the cost function of a single sample for each iteration. Applications of the Gradient Descent method are addressed in [26, 65].
Batch normalization is an essential technique in artificial neural networks. The advantages of the method are improvement in speed, stability, and performance of neural networks. The input layer can be normalized by scaling and adjusting the activation functions. It is a technique by which the inputs for each layer are normalized to deal with the internal covariate, shift problem, i.e., the problem appears in the intermediate layers because, during training, the distribution of the activation functions is constantly changing. This change slows down the training process because each layer needs to learn a new distribution of activation functions in each training step. This method includes: calculating the variance and mean of the layer inputs, normalizing the layer inputs with the help of batch statistics, scaling, and shifting to find the layer’s output [61].
This section addresses some contributions in which game models solve deep learning and artificial intelligence problems. Figure 4 depicts the basic architectures of a simple neural network and deep learning neural network.
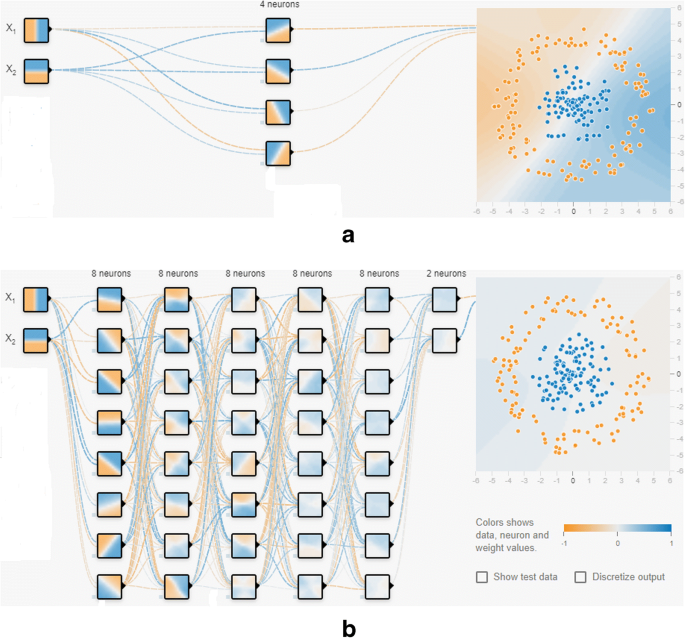
The authors in [112] address a new approach by which game-theoretic techniques can model individual neurons. The authors show that different strategic game-theoretic approaches can be applied to model paired neuron systems. A learning algorithm is developed depending on game theory for neural learning. Artificial neural network has proved its significance in multi-dimensional domains. Selecting an appropriate network is challenging to solve a problem [62, 141, 151]. The authors in [122] show that game-theoretic concepts like the Shapley value help to differentiate significantly from unnecessary elements of an artificial neural network. A cooperative game is designed from a neural network where neurons that form different groups and their contributions to the game are determined with the help of the Shapley value. The experiments prove that the Shapley value concept is better than other heuristics approaches to assess the contribution of neurons.
There are various GAN algorithms. The first is fully connected neural networks for both the generator and discriminator. The second is convolutional GAN, as going from fully connected to convolutional neural networks is a natural extension. The third neural network is conditional GAN. It extends the 2D GAN framework to the conditional setting by making both the generator and the discriminator networks class-conditional [142].
Alternatively, a max-min problem is formulated for adversarial learning with multiplayer stochastic games and two-player sequential games above deep learning networks [17]. The experimental results forecast the efficacy of the used adversarial algorithm. The algorithm can manipulate adversarial features that affect testing results in deep learning models. The work introduces a secure learner who is adaptive to the antagonistic attacks on deep learning. The paper claims that the given framework is more robust than a traditional convolutional neural network (CNN) and a generative adversarial network under adversarial attacks. This paper also highlights the impacts on adversarial payoff functions over randomized strategies while the rules of the games are changed. The offensive scenarios over such strategy spaces find multiplayer games over varied strategies. A reduction of supervised learning to the game is explored in [113]. For convex one-layer problems, an equivalence between Nash equilibria in a simple game and global minimizers of the training problem is shown. It is also demonstrated how the game can be extended to acyclic neural networks using differentiable convex gates. The work in [86] presents a model that integrates the concepts from the field of deep learning and artificial life to reflect their potentiality in various scenarios. The model shows the potentiality of neural networks to simulate population dynamics. The model also shows the applications of evolutionary game theory result in the behavior of the networks.
Modeling humans’ ability to depict the mental state transitions of others is a challenging task for the research community. The authors of [106] train a machine to construct such models. A Theory of Mind neural network (ToMnet) is designed by meta-learning that builds handler models by observing their behavior. The ToMnet model is applied to agents in simple grid environments. This system can autonomously learn modeling other agents, which is a significant contribution to designing multi-agent AI systems. It can be applied to develop technologies for machine-human communication and advance the growth of interpretable artificial intelligence. For large-scale perfect-information games, artificial intelligence is superior to human-level intelligence [124]. On the other hand, it is not easy to find good results in large-scale imperfect-information games (i.e., business strategies, war games, etc.). NFSP is a self-play-based approach without prior information, which helps for effectively learning approximate Nash equilibrium. But, the algorithm depends on Deep Q-Network. In online games, it is not easy to converge by changing opponents’ strategies. Neither in large search scale nor deep search depth games can it find approximate Nash equilibrium. This paper introduces the Monte Carlo Neural Fictitious Self Play (MC-NFSP) algorithm that amalgamates the NFSP and Monte Carlo tree search. For large-scale zero-sum imperfect-information games, the approach improves performance. The asynchronous Neural Fictitious Self Play (ANFSP) model is developed to use a parallel and asynchronous framework to gather the game’s history [145].
The authors in [128] address a reversed reinforcement learning method. After training a deep neural network according to strategies in the payoff table, randomized strategy input is initialized, and the error differentiates the actual output. The required output is propagated back to the initially randomized strategy input in the input layer of the trained deep neural network results in performing a task similar to the human deduction. Detecting imaging biomarkers for autism spectrum disorder (ASD) is challenging to help to explain ASD and predicting or monitoring treatment outcomes. Deep learning classifiers are used to detect ASD from functional magnetic resonance imaging (fMRI) with better correctness than traditional learning strategies. The concept of Shapley value from cooperative game theory is applied to this problem. Cooperative game theory is suitable since it more accurately determines biomarker importance for each instance from deep learning models. The main challenge for using Shapley Value calculation is its computational complexity. The method is validated on the MNIST dataset and compared to human perception. A Random Forest (RF) is modeled is trained to classify ASD or control subjects from fMRI and compare Shapley value outcomes with existing RF-based feature importance [74]. The development of intelligent machine learning applications is studied with expected-long-term profit maximization in multi-agent systems. A learning algorithm for the IPD problem is proposed in [2]. It is shown to outperform the tit-for-tat algorithm and many other adaptive and non-adaptive strategies using numerical analysis. It is also discussed how artificial intelligence and machine learning work closely to provide the agent with a mind-reading capability.
Shin et al. [119] have put forward a model to assign the updating time period to the drones by auctioning. Alternatively, a second-price auction system is applied in which the victorious bidder pays the second-highest bid. In the model, data needed for the dispersal of drones was found from the deep learning algorithm. The shortcoming of the model proposed by Shin and the team was it does not consider two significant criteria; the possibility of increasing the charging station and the uncertainty of charging to the drones at smaller bids. Ren et al. [107] have summarized the representative defenses developed, including adversarial training, randomization-based schemes, de-noising methods, and provable defenses.
Further, to utilize the adversarial training-based intuitive training method, Ren et al. have combined min-max games with deep learning and neural network. Leckie et al. [71] have combined game theory and deep learning to evade jamming attacks in network security. Based on a deep analysis of node behavior characteristics in the opportunistic network, Wang et al. [135] have introduced the evolutionary game theory to traverse the node cooperation mechanism in the opportunistic social network. In the same line, Ranadheera et al. [118] have utilized a deep learning-based deep-Q algorithm with the game theory for fair and efficient resource management in mobile edge computing. To achieve intelligence in the shared environment with multiple agents, Lanctot et al. Further, Lu and Kai [78] have generalized a multi-agent approach using reinforced deep learning and game theory. Dasgupta et al. [21] have combined deep learning and game theory for cybersecurity approaches.
Rudral et al. [108] have used deep learning-based predictive modeling for football games to result in multilayer perception. Wakatsuki et al. (2020) have used multi-player games for decision making. Wang et al. [134] have used the Deep Neural Network (DNN) based deep learning model and the game theory to provide a holistic framework of robot-human interaction. Pinto et al. [104] have used self-supervised deep learning for the robotic adversary. Moreover, they have designed adversarial training as a two-player zero-sum repeated game. Balduzzi [22] has used gradient-based game theory and deep learning to optimize game grammars. Shu et al. [44] have used DNN and game-theoretical approach for developing Multi-granularity Network Representation Learning (MGNRL) framework for the latent representation of nodes in the network. Game theory and deep learning concepts have been widely used in the education field also. Vos et al. [95] have combined game theory and deep learning to understand students’ motivation in education. Urbani [101] has combined game theory and deep learning for music genre classification. Han and Jiequn [63] have concluded that their approach of Deep Learning Approximation for Stochastic Control Problems should apply to broad areas, including dynamic game theory with more than one agent, dynamic resource allocation with several resources and demands, and properties management with large portfolios. Woo [137] has used game-theoretic complex analysis for nuclear security by addressing non-zero-sum algorithms. In the research, Woo has used deep learning for data processing, where the neural network is used for wiretapping. Table 2 summarizes critical game-theoretic models/concepts used to model various deep learning/artificial systems.
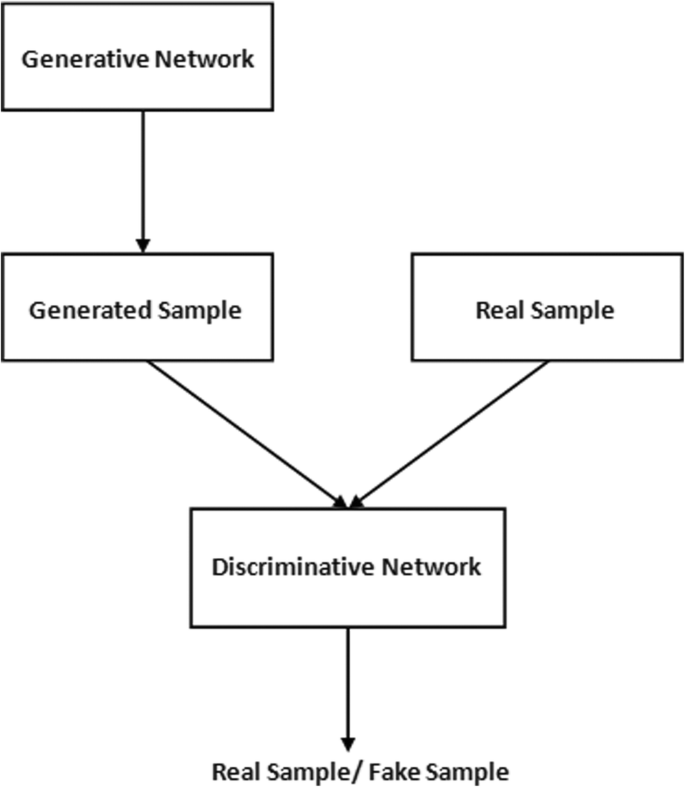
The contribution in [123] sets up a connection amidst a deep learning model and a game-theoretic approach. This work introduces the application of deep learning to solve game-theoretic problems. Some techniques have been addressed to speed up deep learning and gradient-based approaches in actions with continuity for multi-agent adversarial games. On the other hand, multiple GANs are developed as robust distributed games. A Bregman-based strategic deep learning algorithm is introduced for finding robust distributed Nash equilibria, and it is also checked upon in image synthesis and picture classification. GANs are modeled as a min-max game, and a fast learning algorithm using Bregman divergence is explored. A comparative study on the performance of the Bregman-based algorithm with six algorithms is also shown. Table 3 shows a mapping of components of a game with the components of the deep learning network. The work in [16] shows that deep learning is unsafe for changes in data distribution. So, a deep learning network like CNN is dangerous for adversarial scenarios. An adversarial learning model is designed for supervised learning. Adversarial scenarios are modeled by a game-theoretic approach to the conduct of deep learning. A smart antagonist and a deep learning model interact with each other. The interaction is represented as a two-person sequential non-cooperative Stackelberg game, and stochastic payoff functions are formulated.
The datasets used in most of the research articles in this study are as follows: MNIST, CelebA, CIFAR-10, BBBC039, initial dataset, transfer dataset, SVHN, STL-10, ImageNet, DIEL, etc.
The current study mainly focuses on deep reinforcement learning and GAN models. There are various real-time and business applications of GAN and reinforcement learning. The current study addresses several diverse problems. Some significant implementation environments of GAN and deep reinforcement learning models are described in this section based on the existing literature. GAN is primarily used to generate samples/images for various image datasets. GAN can be used to create images of human faces, which are used for different purposes. GANs also help to create realistic images. The cartoon industry is a popular entertainment industry where GAN is used to generate various cartoon characters. Another critical application of GAN is image to image translation. Text to image translation is another vital application of GAN. GAN can be used to generate new human postures which have security, healthcare, and entertainment applications. Another exciting application is generating emojis from typical images frequently used in various social network platforms, mobile applications for entertainment purposes. Photos are edited using GAN models. Photo blending is also done using GAN models. GAN is used for video prediction and 3D object generation. GAN can be used for improving cybersecurity in various places and improving healthcare sectors. It can create artistic skills; it can generate exact or similar images of a painting. It can even cause fake videos. The quality of an image can also be improved using GAN that serves several purposes. De-noising on images is also done using GAN. Alternatively, deep reinforcement learning has excellent application in real-time systems and industries. It is used for the implementation of a self-driving car and industry automation. Deep reinforcement learning is also used in NLP applications. The Healthcare system has also adopted deep reinforcement learning as a tool. It successfully performs various tasks such as automatic disease prediction etc. It has other robust applications in news recommendation and gaming. It also has applications to build automated robots. It has other significant applications such as resource management in computer clusters, traffic light control, web system configuration, advertisement, etc. Reduction in energy consumption, online recommendation systems are some industrial applications.
The performances of the proposed study can be evaluated through Sensitivity, Specificity, recall. Specificity is defined as the proportion of actual negatives, which got predicted as the negative. Sensitivity is a measure of the balance of real positive cases that got expected as positive. The recall is the measure of our model correctly identifying True Positives [87].
The previous sections of the present work discuss the linkages and applications of game theory in deep learning. The current section aims to discuss future research challenges related to the application of game theory in deep learning. To narrate and list out all possible future challenges is a complex task as different literature uses different simulation environments, simulation tools, different data sets, and different experimental conditions. Nevertheless, the current section discusses some of the critical representative future research directions. The future research direction is described in Table 7 below. Table 7 also provides hints, literary way, and association of game theory and deep learning to get the breakthrough in solving future research challenges.
Table 7 Future research challenges and the association of deep learning and game theoryIn conclusion, researchers and scientists have to do extensive developmental research and efforts in the direction described above to overcome the problems and challenges faced by the future of deep learning, such as genomics and medical imaging. Besides, more techniques and further inspiration are required to develop new deep learning approaches. New methodologies for complex and challenging problems would be necessary as collaborative efforts by various research communities need to be carefully addressed.
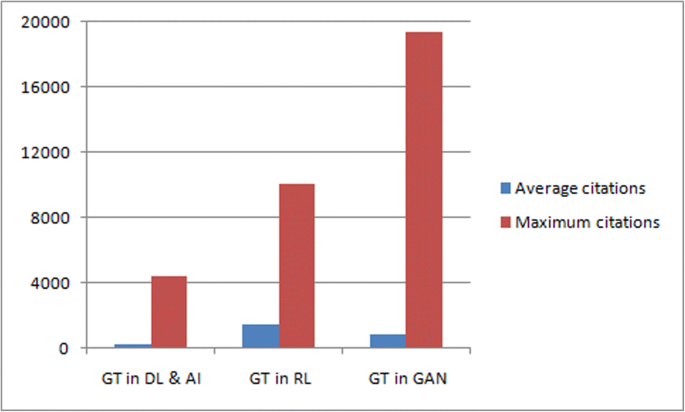
Games play a vital role in the advancement of artificial intelligence. Games are frequently used as training mechanisms in learning algorithms, such as reinforcement learning and imitation learning. The paper highlights that AI-enabled and deep learning-enabled multi-agent systems are also developed to compete or cooperate to complete a goal with the help of game theory. In real-time scenarios, deep learning frameworks need to face situations with imperfect information. Paper considers all 31 articles in which game theory and deep learning coincide described in Table 1. It is discussed in the paper that DeepMind’sAlphaGo works with the help of partial knowledge to strategically make superior to the world’s most efficient human in the game of Go.
The paper also puts ample light on the application of game theory to construct adversarial networks. An essential property of an adversarial network is that a closed-form loss function is not needed. Some networks have the capability of finding their loss function. A significant disadvantage of adversarial networks is difficulties in training them. Adversarial learning models find a Nash equilibrium for a two-player non-cooperative game. The paper addresses applications of game theory in artificial neural networks, reinforcement learning, and deep learning. The main focus is to focus on the construction of GAN by applying different game models. The paper’s contribution may help the researchers in game theory, deep learning, and artificial intelligence to acquire a large number of ideas about inter-domain research and contribute holistic works in these domains. The paper also addresses various challenges and future directions of the identified area that will help researchers explore. In the future, behavioral game theory can be applied to model deep learning networks and mimic human neural networks. The combination of the research areas will open several paths for the researchers.